La topología de diamante

Aún eran tiempos en los que apenas había estudios sobre redes, cuando Internet aún no existía y Arpanet sólo empezaba a balbucear. Cuando pocas personas creaban los protocolos más profundos y arcaicos de la Red. Sin tener el camino marcado aunque con no poca sabiduría, los pioneros teorizaron y experimentaron con las topologías de red que se les ocurrieron.

Uno de los primeros experimentos fue en simuladores que se llevaron a cabo fue en la Lincon Laboratory TX-2 machine. El objetivo de tales experimentos era probar de manera experimental teoremas sobre colas de mensajes en la comunicación, que estaba desarrollando el equipo de Leonard Kleinrock. Algunos de los teoremas eran matemáticamente intratables y fueron necesarias las simulaciones. Además, el experimento también tuvo la finalidad de usarlo a modo de feedback para la inclusión de nuevas ideas en el proyecto.

Y se les ocurrieron varias topologías. No obstante, en la TX-2 el experimento estuvo acotado a cuatro de ellas. Hoy son muy conocidas la topología de estrella, en la que hay un nodo central con nodos conectados a éste para poder comunicarse, y la topología de malla, en la que cada nodo se conecta con todos los nodos de manera igualitaria sin intermediarios para la comunicación. Y las otras dos, que en su día fueron descartadas por las menos eficientes de las cuatro: la topología de diamante y la llamada K-connect. De estas dos, la que me ha parecido más interesante es la topología de diamante y es la que presentaré.

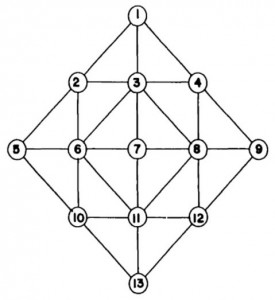
Sin mayor dilación, el diagrama con la topología de diamante que probaron en los experimentos es el siguiente:

Aunque pudiera parecerlo a simple vista, esta topología no es centralizada, o al menos no es centralizadora, ya que ningún nodo es imprescindible para todos los demás. Tampoco es de malla, no todos tienen un enlace directo con todos, pero sí es igualitaria, ya que no es obligatorio que la información de la red pase por un nodo en concreto. Todos los enlaces comunican en ambas direcciones. Pese a que en principio el nodo 7 es aquel que tiene más cerca que cualquier otro su nodo más lejano, los experimentos demostraron que, dependiendo del volumen y destino de los mensajes, en algunos casos podría ser también el que tenga más desventaja, ya que al estar en una posición central, más mensajes pasan por él y mayores colas soporta, por lo que sus propios mensajes, que también se suman al final de la cola, podrían tener un tiempo medio de entrega más alto que los de un nodo periférico.

De manera análoga a las piedras en una partida al juego del Go, en una topología de diamante todos los nodos son iguales a otros y su valor es cambiante dependiendo del estado de la red, es decir, de la relación que tengan los nodos en un momento dado.

En una parte del experimento, los nodos de la topología de diamante tenían tablas de rutas alternas. Cada nodo conocía la ruta que menos saltos requería para llegar a su destino. Si la ruta estaba congestionada, pasaba a la segunda ruta, y así sucesivamente. Si todas lo estaban, el nodo esperaba para retransmitir el mensaje. La ruta más larga quedaba desde el principio descartada. Este planteamiento tenía la ventaja de que tenía un buen rendimiento en condiciones de red ocupada. También experimentaron con tablas de ruta fijas por las que se transmitían los mensaje con independencia del estado de tráfico de la red.

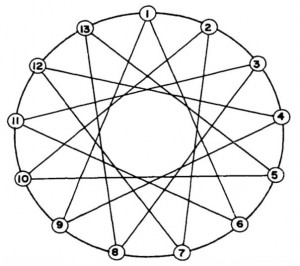
Como corolario al post, para quien no pueda contener su curiosidad ni un segundo más, comparto un diagrama de la topología k-connect.

Tampoco es una topología de malla, ya que no todos conectan con todos, pero cualquier nodo tiene que dar como máximo cuatro saltos para alcanzar su nodo más lejano.

Aunque ésta dos no sean las topologías más eficientes para la transimisión de información en redes de telecomunicaciones, no están exentas de interés, ya que como topologías capaces de estructurar y transportar información, también ocultan estructuras de poder. Su utilidad actual podría estar en el análisis de redes entre personas que se crean espontáneamente o la organización de clusteres en el “big data”. En cualquier caso, dejo el desarrollo de sus aplicaciones a otros más avezados que yo en la materia.

Quién, además, tenga interés en un estudio profundo sobre estas topologías, y tenga un buen nivel de matemáticas, aquí hay una tesis de Kleinrock sobre el retraso en las colas de mensajes.

Ni que decir tiene qué topologías de todas las que participaron en el experimento fueron las seleccionadas  😉